右手之外 看、讀、思考、書寫

855愛的鼓勵 3訂閱站台

 

上星期剛結束場連續三天的學術研討會，我的session排在第三日的午後，上台做完簡報，台下的朋友議論起同一session這幾篇報告人：「就你的論文比較切合實際！」當然身為共同作者的他要這們說，但我口氣裡也不無遺憾的批評那些一直關在學術象牙塔裡的學者專家們，總是不聞世事的低頭做研究，而研討會呢，猶如大拜拜，簡簡單單弄篇學生碩士研究論文，跑跑數值分析、做做實驗，便可輕鬆的擴充自己的論文數目，至於是否能和現實世界發生關係、能不能實際應用，並不在考慮之內。

 

這段話一口氣吐出，回頭再瞧，似乎犯了以偏蓋全的毛病，不過學界與業界的「相看兩厭」也不是一天兩天的事，雖不致齟齬動粗，暗地裡互相批評總是有的。文人相輕自古即然，我如今站在第一線算粗人一個，其實毫無「相輕」的本錢和必要，況且拉遠從人類文明進化的角度看，理論與實際孰輕孰重的問題並不存在，尤其科學的進展一直以來都是互有領先、相互驗證並互補不足，所以我也不過在熟人面前稍稍傾倒些「二十一世紀目睹之怪現象」，並不作任何輕重評判。

 

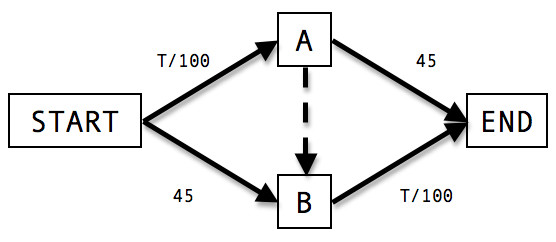
講一個有趣的理論，2009年3月號《科學人》曾作過介紹。參考圖，一個簡化的交通模型，實線上的算式及數字代表車輛行駛通過所需時間。假設有4000輛車自START位置，經由A或B點到達END，當A到B的捷徑（即虛線部份）未開通前，兩條路徑所需花費時間分別為A/100+45、45+B/100，其中A和B分別代表通過的車輛數。如果兩條路徑長度大致相同的話，駕駛人選擇任一路徑的機率均相同，因此需花費2000/100+45＝65分鐘。

 

當自A到B的新道路開闢後，假設此快捷道路距離極短，可忽略通過時間，此時駕駛人會如何選擇？很顯然，最佳路徑將會是經由A到B再開往目的地，但如果人同此心、心同此理，則4000輛車同時擠上同一條路，總共需花費4000/100+4000/100＝80分鐘的時間，比新道路未開闢前還要多了15分鐘！

 

這看似與生活常理相異的結論，是由德國的數學家柏拉斯（Dietrich Braess）於1968年所證明的概念，稱之為「柏拉斯悖論（The Braess Paradox）」。純粹數學可證明，在自利心的作用下，個人的最佳化選擇並不等同於整體的最佳化，簡單的用交通管制的角度看，增加道路建設的確提供用路人較多的便利選擇，只是一旦所有的人同時擠入最佳選擇，反而造成交通大擁塞。這種理論既稱「悖論」，便是不能以常理度之，依一般人對數學的不熟悉和不信任，模型不僅過於簡化，且忽略了用路人的心理因素。不過2003年南韓的首爾在當年的市長、也是現任總統的推動下，將原來長5.8公里的的高架高速公路拆除，恢復了既有河道，市區交通反而得到改善，成為「柏拉斯悖論」的反向證明，顯然無論交通管制專家或用路人都有必要重新檢視，是不是可以運用這種悖離常理的概念，藉著限制汽車路權來改善整體交通？譬如台北市目前封閉整修中的新生高架橋，歷經三、四十年來的使用，已如都市盲腸般的醜陋，有誰敢大刀闊斧的拆除，恢復瑠公圳的舊時原貌？

 

數學最有意思的一件事，莫過於和生活直覺上的相互抵觸了，再多談一個例子。MLB今年球季開打前（請不要跟我ERA高達30好幾的Chien-Ming Wang），洋基隊為了是不是將隊長Jeter和Damon的棒次互調而傷透腦筋，網路上的好事者不作無謂的口水爭執，而是直接拿統計數字作回歸計算，譬如有人在壘的打擊率（OBP, on-base percentage）、長打率（SLG , slugging percentage）與每場得分（R/G）的關係可回歸如下（註）：

 

R/G = 17.11*OBP + 11.13*SLG - 5.66

 

根據計算，當Jeter打第一棒而和Damon打第二棒時，洋基隊每場球可多得0.02分，整季球賽則可增加約3分！！

 

"In God we trust, everyone else brings data! "這句老美常掛在口中的諺語，說明了數字崇拜者實事求是的精神，不過再怎麼樣，我大概也無法將數字和宗教等同並列。但數字確實有其可供迷戀之處，當理論物理學家談起「量子纏結」、「薛丁格的貓」或是玄到九玄天外的「弦論」時候，我只能豎立致敬，不敢多發一語。

 

註：Baseball Musings 於3/26/’09的文章 "LINEUP CHANGE (http://baseballmusings.com/?p=30923)"