
從國中到高中,數學的難度如斷層般提高不少,小孩喜歡挑戰我的權威,所以時時拋出題目向我「請教」。高一學期末教到對數,利用對數的四則運算,配合著指數、二元二次方程式,可變化組合出許多看似毫無道理的難題,每個題目都需要一些訣竅去破解。只是這些破解技巧,多不屬邏輯所能推導,必須靈光一閃,或經一再的熟習,又或是補習班名師的講解。於普通人觀之,除了鍛鍊腦力之外(譬如參加數學奧林匹亞競賽),和日常生活毫不相干,也因此成為許多人自小畏懼數學的原因,並不斷讓人質疑:學了又如何?不會又如何?
回想自己的數學學習過程,小學與國中只能稱作「算數」,用於熟悉數字及其運算原則,高中一開始便是相當陌生的「數論」,因得初窺「數學」領域,其後三角幾何、多元多次以及機率、邏輯、統計和微積分理論一路學習下來,多是懵懵懂懂,必須到大學、研究所階段的工程數學方與實務結合,也多少才瞭解其價值所在,可從來就不曾拉高視野去探究「數學」堂奧。舉例而言,就幾何領域,歐基里德的「幾何原本Elements」堪稱極重要的基礎,但國中、甚至高中老師在考試引導教學的大綱下,從未真正教授過,以致於我對所謂定義、公設和證明的理解,居然遲到讀完這本「爺爺的證明題」才窺得其邏輯脈絡。
「爺爺的證明題」以兩條主線書寫,其一是大學教授的課程「思考無限」,以數學領域中的「無限」數論遍及哲學思維;另一條主線則發生在幾十年前,從探究主角爺爺身陷牢獄的原由,一步步揭開一場宗教vs數學的反覆辯證。中文譯著的副標題「上帝存在嗎?」頗具戰帖意味,不過英文書名的副標題只簡簡單單的A Mathematical Novel。就我讀過的「數學小說」而言,「博士熱愛的算式」猶如小學生般擺弄數字,看似奇炫,其實無太多道理可堪探究,且其書寫邏輯大有問題。相對的,這本書談論的數學理論十分值得思索,尤其是有關「無限」的度量問題讓我大開眼界,讓我理解原來所謂的「無限」仍存在可相互比較的尺度。但更重要的是,它利用一套嚴謹的推理模式,意圖解決宗教問題,雖然這部分我早已建構出「科學的歸科學、宗教的歸宗教」這一套簡單的原則,仍有許多可觀處,其中之一,便是「歐式幾何」與「非歐幾何」的差異。
現代平面幾何並非肇始自「幾何原本」,歐基里德僅著力於集大成,但因此奠定數學的嚴謹美學成為他最大的貢獻。在「幾何原本」書中,歐式利用23個定義(譬如點沒有面積、線只有長度而沒有寬度、線的兩端是點等等),5條不證自明的公設(書中譯作「設準」,但這兩個字很不數學,我仍是偏好「公設」),包括:
1. 由任意一點向另一點可做直線;
2. 一條直線可以被延長;
3. 以任意圓心和任意半徑可做圓;
4. 直角皆相等;
5. 同一平面內一直線於另外兩條直線相交,如果同一側相交所成的兩內角之和小於二直角,那麼這兩條直線於這一側相交。
便足以推導出包括三角形的相似、全等,以及我們熟知的「畢氏定理」等種種定理。這種由簡至繁的推理方式,唯一的依靠就是縝密的邏輯方法,也因此讓數學成為科學重要的支柱,甚至賦予了它莊嚴堂皇之美。
「歐式幾何」揭櫫了邏輯的真善美,但從上述有關「公設」的敘述中可發現,公設5(平行公設)落落長的說明,顯然和前4則公設大大不同,不斷讓後人思忖到底需不需要這一則公設?單靠前4則公設,夠不夠證明出公設5?這種種懷疑和研究延續千年,也因而發展出一套「非歐幾何」。書中舉了一個典型的非歐幾何模型,如圖:
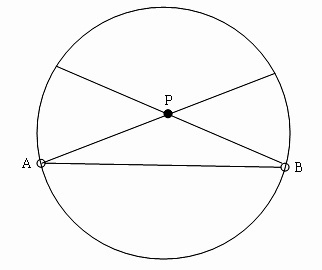
定義此圓為一平面,但圓的邊緣不屬於平面,所以點A、B分別用小圓圈取代。P點是平面上位於直線AB外部的一點,通過P點可作2條直線PA、PB,但由於A、B不在平面上,所以不論PA或PB都不與AB相交,也就是說,按照平行線的定義,PA、PB和AB相互平行,在我們的直觀中是完全不可能的!
為什麼「非歐幾何」如此重要?因為它打破了我們對平面世界的直觀想像,在「爺爺的證明題」一書中,也成為身陷囚籠的爺爺和法官之間相互解套的模型。爺爺是來自印度的訪問學者,秉持嚴謹的數學邏輯精神,因基督信仰並無法找到ㄧ個「不證自明」的起始「公設」,所以拒絕承認上帝的存在,而被當時的美國法律訴以褻瀆上帝之罪。法官在訪談中,爺爺藉「歐式幾何」向法官展示數學邏輯之美,而身為虔誠信徒的法官雖瞭解爺爺的立論,也一心希望能不起訴他,但卻遲遲無法找到打破這套邏輯的方法。這糾纏多時的辨證,終於在翻找出「非歐幾何」,以及在愛因斯坦的相對論證據得到實驗證明之後(重力引致之光曲現象),兩人都透了一口氣,各自安心了,因為邏輯之美依舊存在,只是起始定義不同而已,數學與信仰也因此可各自尋得安身立命的處所,而毋須相互攻擊。
原著書名A Certain Ambiguity(我譯做「確定的模糊」)很值得深思。數理邏輯並不存在模糊空間,「違反邏輯」在理論推導時可視作反向證明,這種嚴謹態度也出現在信仰一事,因為「上帝的存在」同樣不容模糊。只是當兩者碰撞、相互質疑和挑戰時,兩敗俱傷是一種解決方式,而另一種,大致便是如同此書的結尾,同中求異且異中求同,各自退讓一步便能找出彼此同享存在的模糊空間。這是一本具相當難度的小說,作者雖說明了書中數學部份可為一般讀者接受,但我相信若非具有理工背景,「無限」概念和數學證明所形成的高門檻絕對會讓人心生畏懼,不過若能跨過,可輕易在作者信手拈來,或偽作的歷史典故中,挖掘出不少屬於自己的推理樂趣。
文章定位:




