In order to understand early civilizations, archaeologists often study texts written in
ancient languages. One such language, used in Egypt more than 3000 years ago, is based
on characters called hieroglyphs. Figure C.1 shows six hieroglyphs and their names. In
this problem, you will write a program to recognize these six characters.
Figure C.1: Six hieroglyphs
The input consists of several test cases, each of which describes an image containing
one or more hieroglyphs chosen from among those shown in Figure C.1. The image is given
in the form of a series of horizontal scan lines consisting of black pixels (represented
by 1) and white pixels (represented by 0). In the input data, each scan line is encoded
in hexadecimal notation. For example, the sequence of eight pixels 10011100
(one black pixel, followed by two white pixels, and so on) would be represented in hexadecimal
notation as 9c. Only digits and lowercase letters a through f are used
in the hexadecimal encoding. The first line of each test case contains two integers,
H and W. H
(0 < H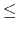
200) is the number of scan lines in the image. W
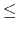(0 < W50) is the number of hexadecimal characters in each line. The next H lines
contain the hexadecimal characters of the image, working from top to bottom. Input images
conform to the following rules:
- The image contains only hieroglyphs shown in Figure C.1.
- Each image contains at least one valid hieroglyph.
- Each black pixel in the image is part of a valid hieroglyph.
- Each hieroglyph consists of a connected set of black pixels and each black pixel
has at least one other black pixel on its top, bottom, left, or right side.
- The hieroglyphs do not touch and no hieroglyph is inside another hieroglyph.
- Two black pixels that touch diagonally will always have a common touching black pixel.
- The hieroglyphs may be distorted but each has a shape that is topologically equivalent
to one of the symbols in Figure C.1. (Two figures are topologically equivalent if each can
be transformed into the other by stretching without tearing.)
The last test case is followed by a line containing two zeros.
For each test case, display its case number followed by a string containing one character
for each hieroglyph recognized in the image, using the following code:
Ankh: A
Wedjat: J
Djed: D
Scarab: S
Was: W
Akhet: K
In each output string, print the codes in alphabetic order. Follow the format of the sample
output.
The sample input contains descriptions of test cases shown in Figures C.2 and C.3.
Due to space constraints not all of the sample input can be shown on this page.
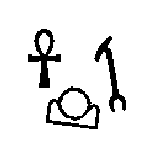
100 25
0000000000000000000000000
0000000000000000000000000
...(50 lines omitted)...
00001fe0000000000007c0000
00003fe0000000000007c0000
...(44 lines omitted)...
0000000000000000000000000
0000000000000000000000000
150 38
00000000000000000000000000000000000000
00000000000000000000000000000000000000
...(75 lines omitted)...
0000000003fffffffffffffffff00000000000
0000000003fffffffffffffffff00000000000
...(69 lines omitted)...
00000000000000000000000000000000000000
00000000000000000000000000000000000000
0 0
Case 1: AKW
Case 2: AAAAA
題目描述：
圖形只會有黑白兩色，但是輸入格式則是壓成 bytes，而如果是同一個象形文字，則黑色的 pixel 會藉由上下左右相連，而象形文字間不會相碰，題目要求辨識圖形中所有的象形文字，輸出的時候按照字典順序。
題目解法：
很特別的是，當看一個圖形時，白色區塊的個數剛好是 0-5，那麼就藉此區分圖形。
首先，先將外圍補上白色，然後將不屬於內部的白色塗滿，用以分開所有的象形文字。
由於黑色是按照上下左右，那外圍白色則是八個方位。
跟著去找一個黑色的 pixel 當作一個象形文字，找鄰近且非外部白色進行塗色計算白色區域，
此時的白色區域是上下左右而已。
這麼做就可以找到所有象形文字的白色區塊個數。
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
char g[205][505], cg[205][505], used[205][505];
int n, m, white_space;
void wdfs(int x, int y) {
if(x < 0 || y < 0 || x >= n || y >= m)
return;
if(g[x][y] != 0 || used[x][y])
return;
used[x][y] = 1, cg[x][y] = 3;
wdfs(x+1, y);
wdfs(x-1, y);
wdfs(x, y+1);
wdfs(x, y-1);
}
int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};
void dfs(int x, int y) {
if(x < 0 || y < 0 || x >= n || y >= m)
return;
if(g[x][y] != 1 || used[x][y])
return;
used[x][y] = 1, cg[x][y] = 2;
dfs(x+1, y);
dfs(x-1, y);
dfs(x, y+1);
dfs(x, y-1);
int i, tx, ty;
for(i = 0; i < 4; i++) {
tx = x+dx[i], ty = y+dy[i];
if(tx < 0 || ty < 0 || tx >= n || ty >= m)
continue;
if(g[tx][ty] == 0 && used[tx][ty] == 0) {
white_space++;
wdfs(tx, ty);
}
}
}
void bdfs(int x, int y) {
if(x < 0 || y < 0 || x >= n || y >= m)
return;
if(g[x][y] != 0 || used[x][y])
return;
used[x][y] = 1, cg[x][y] = 1;
bdfs(x, y+1);
bdfs(x, y-1);
bdfs(x+1, y+1);
bdfs(x+1, y);
bdfs(x+1, y-1);
bdfs(x-1, y+1);
bdfs(x-1, y);
bdfs(x-1, y-1);
}
int main() {
int cases = 0, h, w;
char s[205];
while(scanf("%d %d", &h, &w) == 2 && w) {
int i, j, k;
memset(g, 0, sizeof(g));
memset(cg, 0, sizeof(cg));
memset(used, 0, sizeof(used));
for(i = 1; i <= h; i++) {
scanf("%s", s+1);
int idx = 0;
s[0] = '0';
s[strlen(s)] = '0';
s[strlen(s)+1] = '\0';
for(j = 0; s[j]; j++) {
int v = s[j] <= '9' ? (s[j]-'0') : (s[j]-'a'+10);
for(k = 3; k >= 0; k--)
g[i][idx++] = (v>>k)&1;
}
}
n = h+2, m = w*4+8;
bdfs(0, 0);//bound color
char ret[1005];
int retidx = 0;
for(i = 0; i < n; i++) {
for(j = 0; j < m; j++) {
if(g[i][j] == 1 && used[i][j] == 0) {
white_space = 0;
dfs(i, j);
switch(white_space) {
case 0:ret[retidx++] = 'W';break;
case 1:ret[retidx++] = 'A';break;
case 2:ret[retidx++] = 'K';break;
case 3:ret[retidx++] = 'J';break;
case 4:ret[retidx++] = 'S';break;
case 5:ret[retidx++] = 'D';break;
}
}
}
}
sort(ret, ret+retidx);
printf("Case %d: ", ++cases);
for(i = 0; i < retidx; i++)
putchar(ret[i]);
puts("");
/*for(i = 0; i < h; i++, puts("")) {
for(j = 0; j < 4*w+4; j++)
printf("%d", g[i][j]);
}*/
}
return 0;
}
文章定位：
