The world of sakanaimmune 我從來就知道失去是怎麼一回事, 我只是從來就不喜歡面對失去而已. from橘子

218愛的鼓勵 0訂閱站台

康明昌

諾貝爾獎為什麼沒有包括數學這一學門？對於這個問題有不少揣測。例如，有人說，諾貝爾（A.B. Nobel, 1833～1896年）與當時斯德哥爾摩大學的數學教授 M.G. Mittag-Leffler（1846年～1927年）有嫌隙，諾貝爾不想設個諾貝爾數學獎的目的正是要防止 Mittag-Leffler 得獎。儘管這類揣測都經不起事實的考驗，它們仍然是茶餘飯後大家喜歡談論的話題。

可是在數學家之間，也有一個像諾貝爾獎那麼崇高的獎，那就是費爾茲獎 (Fields medals) 與奈望林納獎 (Nevanlinna prize)。

費爾茲獎是根據加拿大多倫多大學教授費爾茲（J.C. Fields, 1863～1932年）的遺囑與捐贈成立的。它的全名是國際數學傑出成就獎 (The International Medals for Outstanding Discoveries in Mathematics)。自1936年首次頒獎，然後因第二次世界大戰中輟16年，1950年起，每四年召開一次國際數學家會議，每次頒授二到四位費爾茲獎的得主。費爾茲獎授予對當代數學有傑出貢獻者，以鼓勵他們繼續完成更偉大的科學成就。雖然沒有明文規定，費爾茲獎得主的年齡一向不超過四十歲。到目前為止，共有34位費爾茲獎的得主，其中只有四個東方人：日本的小平邦彥（1954年）、廣中平祐（1970年）、森重文（1990年）與我國的丘成桐（1983年）。

奈望林納獎由芬蘭赫爾辛基大學提供基金，為紀念芬蘭數學家奈望林納（R. Nevanlinna, 1895～1980年）設立的。奈望林納獎的目的是獎勵在資訊科學的數學理論有傑出貢獻的學者。到目前為止，共有三位奈望林納獎的得主。

費爾茲是加拿大人，1887年在美國約翰霍浦金斯大學獲得博士學位。1902年起任教於加拿大多倫多大學，他是1924年國際數學家會議在加拿大多倫多舉行時的大會主席。費爾茲本人的數學研究相當優異，他曾被選為英國皇家學會的會員，但是現在人們還記得他的原因恐怕是由於他設立的這個數學大獎。

奈望林納是當代傑出的複變函數論學者。他在1920年代建立亞純函數的值分布理論。奈望林納的理論後來被推廣到多複變函數與算術幾何，是九十年代頗受矚目的一支數學理論。第一屆費爾茲獎得主之一 L.V. Ahlfors 是奈望林納的學生。

1990年的國際數學家會議，於八月二十一至二十九日在日本京都舉行。

京都是日本的古都（794～1868年），794年桓武天皇把國都自奈良遷來京都，並仿照當時唐朝的長安建造京都的城門與街道。這是一個保留許多日本傳統文化的城市，日本文學家川端康成的小說《古都》與谷崎潤一郎的小說《細雪》，都以京都為背景。

這次京都的國際數學家會議誕生了四個費爾茲獎的得主：森重文 (S. Mori)、德林斐特 (V.G. Drinfeld)、鍾斯 (V.F.R. Jones) 與維騰 (E. Witten)。在十八、十九世紀數學家與物理學家一直是密切合作的朋友，可是二十世紀的數學與物理似乎變成互不往來的兩個世界，這種分離的局面看樣子快結束了：在這次費爾茲獎的得主，除了森重文之外，其餘三人的研究領域和數學物理都有密切的聯繫。在另一方面，計算機科學對數學的影響似乎不如物理，在四年前柏克萊的國際數學家會議，曾有記者問起四位得獎人（費爾茲獎的 Donaldson、Faltings、 Freedman 與奈望林納獎的 Valiant），計算機的出現對他們的研究工作有何影響？三個費爾茲獎得主回答：「毫無用處」，研究資訊科學理論的 Valiant 居然承認，他也不用計算機。

森重文，1951～

森重文，1951年生於日本名古屋。1969年因東京大學鬧學潮停收新生，乃投考京都大學，1978年獲得京都大學博士學位，指導教授為永田雅宜 (M. Nagata)，博士論文是與交換簇的 Tate 猜測有關的問題。森重文曾任教名古屋大學、美國哥倫比亞大學、猶他大學，現在是京都大學數理解析研究所教授。森重文近年得獎無數，今年年初獲得美國數學會代數的大獎 Cole 獎，其後與學習院大學的飯高茂 (S. Iitaka)、東京大學的川又雄二郎 (Y. Kawamata) 共同得到日本科學院獎。這次得到費爾茲獎，許多人並不感意外。

森重文的工作集中在代數幾何，尤其是三維代數多樣體的極小模型。在一維多樣體時，虧格便足以分類平滑的射影曲線，這是十九世紀數學家熟知的。二維代數多樣體的分類工作就難得多了，這工作基本上是本世紀前二十年由義大利數學家 F. Enriques（1871～1946年）完成的，1960年前後 Zariski 與小平邦彥做了一些推廣。可以說，從1920～1970年幾乎沒有人知道三維多樣體的分類該從何著手。森重文的成就差不多是劃時代的工作，他證明三維極小模型的存在定理，並且建立高維多樣體極小模型的理論。

V.F.R. Jones, 1952～

鍾斯，1952年生於紐西蘭，1979獲得瑞士日內瓦大學博士學位，指導教授為 A. Haefliger。他曾任教於美國賓州大學，現在是加州大學柏克萊校區的教授。

鍾斯的研究主題最先是 C^* 代數。他在不可解的 von Neumann 代數的子代數引入指標的概念，他發現當指標小於4時，它只可能是 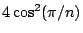(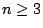)。這些數引出研究李代數時無所不在的 Coxeter-Dynkin 圖表，從此展開了 von Neumann 代數研究的里程碑：他研究辮群與 Hecke 代數的關係，因而發現鍾斯多項式。鍾斯多項式現在變成拓撲學家研究紐結理論的重要工具。在另一方面，它與 Chern-Simons 形式（Chern 指陳省身先生）、保角場論、拓樸場論也具有相當密切的關係。

V.G. Drinfeld, 1954～

德林斐特是蘇聯人，1954年生，目前任職於蘇聯科學院烏克蘭分院的低溫物理與工程研究所。

德林斐特的研究領域跨代數數論與數學物理兩個分支。在本世紀初許多人早已發現代數數論與大域函數體有許多類似的性質，但是卻無人知道如何具體的呈現這些相似點，德林斐特在他的博士論文引入德林斐特模的概念，使得大域函數體也能夠像代數數體一樣運用分析的工具從事研究。此外，德林斐特又證明有名的 Langland 猜測的幾個特例。在數學物理方面，他的成就也極為傑出，尤其在量子群。Drinfeld 曾研究 N 瞬息子解的結構，將孤立子方程系統化，並解決古典的 Yang-Baxter 方程（Yang 指楊振寧先生）解的分類問題。

E. Witten, 1951～

維騰，1951年生於美國，1976年獲得美國普林斯頓大學物理博士學位，指導教授為 D. Gross，博士論文是與粒子物理現象學有關的。維騰在1976～1980年到哈佛大學從事博士後研究，這時已展現他在量子場論超人的想像與理解力，因此，普林斯頓大學於1980年聘請他回去擔任物理系教授。維騰的父親 L. Witten 也是個物理學家，在美國辛辛那提大學任教，研究重點是古典重力理論。

1980年代初期理論物理的一個主要研究方向是超對稱。維騰首先用 Atiyah-Singer 指標定理研究超對稱的自發失稱，其後他的研究重點集中在超弦理論。他利用超對稱的概念探討各種數學問題，對於許多有名的數學定理，如 Atiyah-Singer 指標定理、Morse 不等式、丘成桐與 Shoen 的正質量定理、Donaldson 多項式、鍾斯多項式，維騰都有新的觀點或證明。就像十九世紀德國數學家黎曼（B. Riemann, 1826～1866年）運用豐富的物理直覺，研究複變函數論，維騰的工作使數學和物理重新搭起一座橋樑，並且它描繪出一個許多人未曾夢想過的世界，誰敢說那不是下一代數學家探索的新方向之一呢？

得過費爾茲獎的東方人只有四位：小平邦彥（1954年）、廣中平祐（1970年）、邱成桐（1983年）、森重文（1990年）。

小平邦彥，1917～1997

小平邦彥，1915年生於東京，他在東京帝大念數學（1938年）與理論物理（1941年），取得兩個學士學位，1949年東京大學博士，他的博士論文討論黎曼流形的調和形式。他從1944年擔任東京大學數學系助教授，1949年之後陸續在美國普林斯頓高級研究所、普林斯頓大學、哈佛大學、約翰霍浦金斯大學、史丹福大學任教，直到1967年才回到東京大學任教。小平邦彥在1957年獲頒日本科學院獎與日本文化界的最高榮譽「文化勳章」，1965年入選為日本科學院院士。

小平邦彥的主要工作集中在代數幾何與複流形，他在 Riemann-Roch 定理、複流形的變形理論、代數曲面與解析曲面的分類與結構，都有非常重要而且深遠的貢獻。

廣中平祐，1931～

廣中平祐，1931年生於日本山口縣，畢業於日本京都大學（理學士，1954年；理學碩士，1957年）。1957年代數幾何大師 O. Zariski（1899～1986年）赴日講學，廣中平祐經由京都大學秋月康夫教授 (Y. Akizuki) 的介紹，乃隨 Zariski 到美國哈佛大學就讀，1960年獲博士學位。1964年廣中平祐成功的解決古典域中奇異點集的化解問題。廣中平祐自1968年任教於哈佛大學，1970年獲得日本科學院獎，1975年日本政府贈予「文化勳章」，1976年入選為日本科學院院士。

奇異點集化解問題是代數幾何與複幾何的大問題。由於這問題難度太高，研究此問題的數學家並不多，但是其重要性卻是大家深信不疑的。廣中平祐從畢業後即全力研究奇異點集問題，其放手一搏的膽識與毅力實在值得後輩景仰師法。廣中平祐於1987年應國科會邀請，來我國做短期訪問演講。

丘成桐，1949～

丘成桐，1949年生於廣東汕頭市。後隨家人移居香港，就讀於香港中文大學，其後到美國加州大學柏克萊校區受業於當代微分幾何大師陳省身先生，1971年獲得博士學位。1981年獲得美國數學會幾何的大獎 Veblen 獎，1986年當選中央研究院院士。丘成桐曾任教於紐約州立大學石溪分校、史丹福大學、普林斯頓高級研究所、加州大學聖地牙哥校區，現任教於哈佛大學。

丘成桐成功的把微分幾何與偏微分方程的技巧與理論結合在一起，他解決許多有名的猜想，在偏微分方程、微分幾何、複幾何、代數幾何、以及廣義相對論，都有永不磨滅的貢獻。

後記：本文承蒙台灣大學賴東昇先生、黃偉彥先生，清華大學顏晃徹先生、高涌泉先生，中正大學鄭國順先生提供許多重要資料與寶貴意見，謹此誌謝。